How I Handle Puzzle Solving and Validation: Generating a Sudoku Grid in Kotlin

It has been some time since I wrote about my project on this blog. A few days ago, I was working on features for another project, and then I caught the flu. I was so tired and sick that I spent some time watching the Supernatural series. It was good.

This week, I’m back on track and feeling better—not great, but better. I am finishing my Android Sudoku application, so I plan a series of articles about Sudoku and my project. Last time, I wrote about the backtracking algorithm. Today, this article will focus on Sudoku solving and validation. So—stay tuned!

Overview

When working on logic-based games, Sudoku stands out as a great puzzle to challenge the player and test my algorithmic thinking. In this post, I’ll walk you through how I approached generating a complete Sudoku puzzle using Kotlin, focusing on the structure, validation, and recursive solving strategy behind it.

The Goal: Generate a Complete Sudoku Grid

My goal is simple and clear: to generate a Sudoku grid that satisfies these rules:

1. Each row must contain numbers 1–9 without repetition.
2. Each column must contain numbers 1–9 without repetition.
3. Each 3×3 box must contain numbers 1–9 without repetition.

To do this, I used backtracking, a classic technique for solving constraint satisfaction problems. I discussed backtracking in my previous article, but today I’ll add some code examples.

Generating the Sudoku Grid

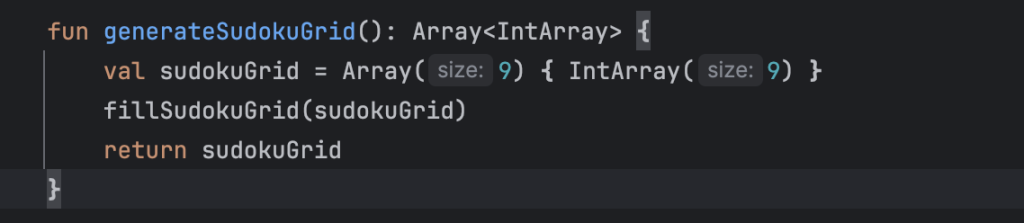
The code creates a simple, empty 9×9 matrix, then calls the fillSudokuGrid(), which uses recursive backtracking to fill the grid.

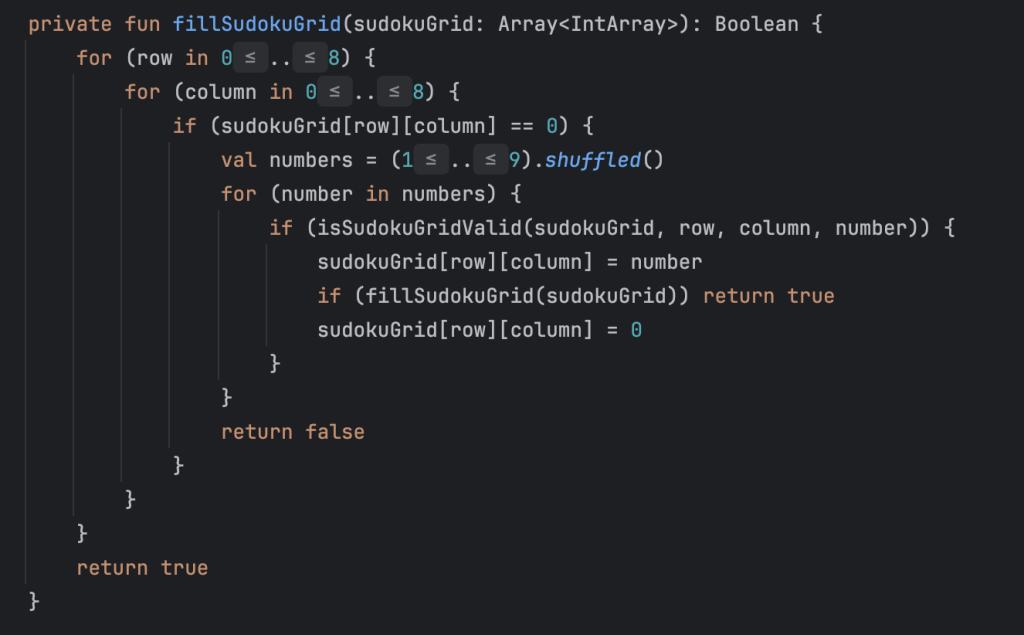
For each empty cell (initialized as 0), I attempt to place a number between 1 and 9, shuffled randomly to add variability. If the number is valid at that position, we recursively attempt to fill the rest of the grid. If we hit a dead end, we backtrack and try the next number. This process is essentially a depth-first search through the solution space.

Validation Logic

This was my favorite part. A number is only placed if it’s valid, ensured by a function that delegates to three checks:

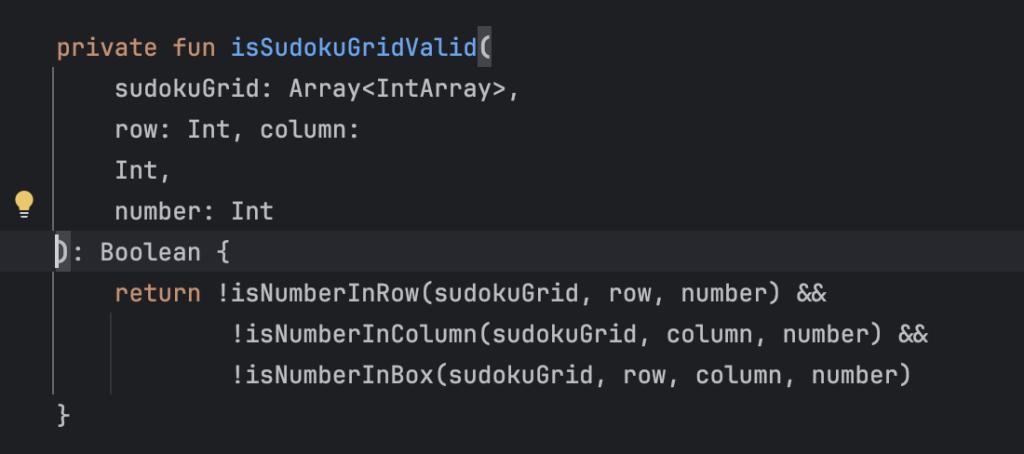
• Row check
• Column check
• 3×3 box check

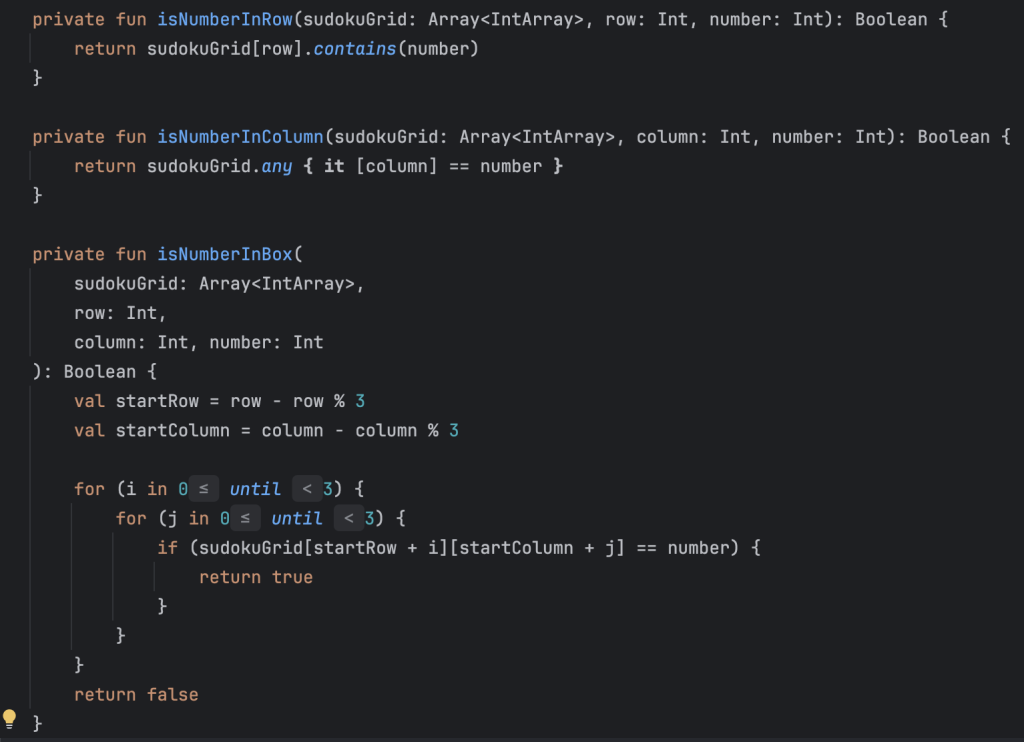
These modular checks make validation easy to test and maintain.

Why This Approach Works

The recursive backtracking approach is powerful for puzzles like Sudoku because it:

• Explores all possible configurations
• Prunes invalid paths early (thanks to validation)
• Guarantees a solution if one exists

It does come with performance costs on larger puzzles or if extended for puzzle difficulty tuning, but for generating valid full boards, it’s efficient enough.

First Step in My Sudoku Logic

This is just the first step in the Sudoku logic. It’s one of the UseCases in my Sudoku application for Android, which you can find here: Neurodoku on GitHub.

Conclusion

By using recursive backtracking and modular validation, I built a Sudoku puzzle generator that guarantees correctness. The algorithm is clear, testable, and surprisingly elegant in its logic.

If you’re working on puzzles, constraint satisfaction, or logic games, this structure might be useful for your own projects.