Welcome to the world of Sudoku and backtracking.
When I first started building a Sudoku game, I didn’t know what to expect. Solving Sudoku puzzles is fun – there are a few rules, nine numbers, and the challenge of filling out a 9×9 grid.
But writing a program that can generate a valid Sudoku grid? That’s a whole different level.
In my first version of the game, I used a simple algorithm: I placed numbers one by one – starting with 1, then 2, and so on – trying to fill every row, column, and 3×3 box.
It worked… sort of. But as a Sudoku fan, I knew there had to be a better, more elegant way.
That’s when I discovered backtracking.
Backtracking: Try Everything (and Then Some)
Backtracking is an algorithmic technique that tries everything – until it finds a valid solution.
When it hits a dead end, it simply goes back (tracks back) and tries a different path.
Let’s say you’re solving a Sudoku puzzle. You find an empty cell – what do you do?
Try 1. Doesn’t work? Try 2. Still doesn’t work? Try 3… and so on, up to 9.
If none of the values work, backtrack to the previous cell and try a different value there.
This process continues until the puzzle is solved – or until you’ve tried every possible option.
Recursion: A Problem That Solves Itself
Backtracking often uses recursion – when a function calls itself.
In my Sudoku generator, each call processes a row and a column in the grid.
If the function encounters an invalid state, it returns to the previous step and tries a new number (like resetting the cell: sudokuGrid[row][column] = 0).
Recursion helps break the problem down into smaller, more manageable parts – each solving a tiny piece of the puzzle.
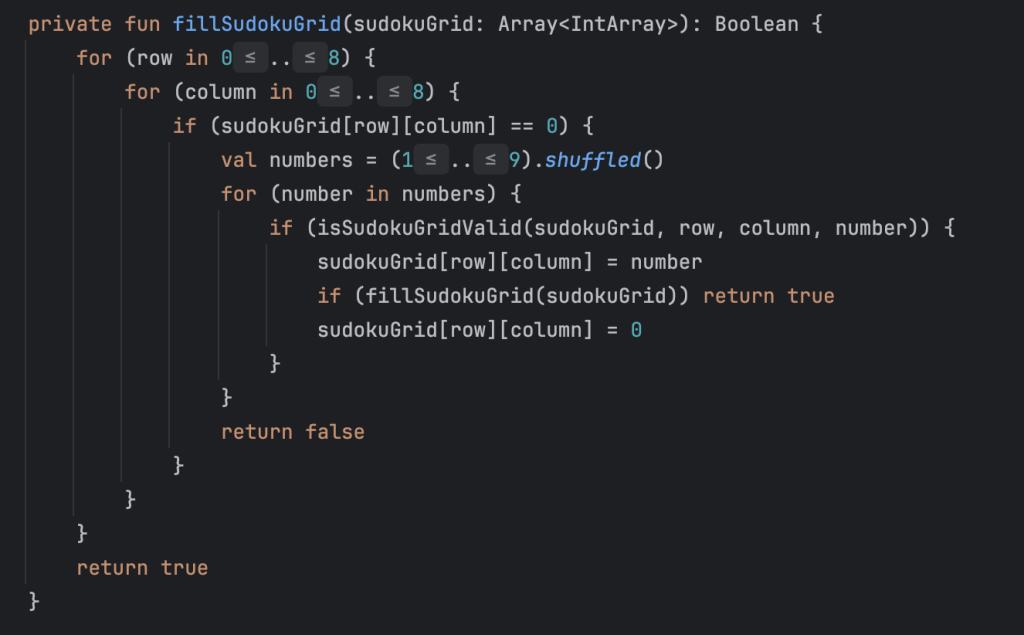
Step by Step – and Try Again
Imagine trying to solve a Sudoku puzzle programmatically. You begin with number 1… it doesn’t fit.
Okay, try 2. Still doesn’t work? Onward to 3… and so on.
Check out the function isSudokuGridValid. It validates each step.
If it fails, the algorithm backtracks and starts again with a new number.
Want a real-life example?
When I renovated my home office, I placed the desk in a “perfect” spot… only to find out it didn’t work at all.
So I moved it. Then again. And again. Until finally, it clicked.
Backtracking, right there in action.
Conclusion: Trust the Process
Whenever you face a problem that feels impossible to solve, remember: backtracking is your friend.
Try, evaluate, step back, and try again.
Sometimes, the right answer shows up on your fifth attempt – and that’s totally okay.
Leave a Reply